Pengertian Fungsi

FUNGSI RASIONAL

FUNGSI

1. FUNGSI RASIONAL

DEFENISI FUNGSI RASIONAL :

fungsi yang memetakan suatu bilangan real x ke bilangan rasional . dengan dan  adalah polinom-polinom dan h(x) tidak sama dengan nol.
Contoh fungsi rasional, 

Fungsi rasional ada dua macam. Yaitu FUNGSI RASONAL BULAT dan FUNGSI RASIONAL PECAHAN

A. FUNGSI RASIONAL BULAT

Fungsi rasional bulat ini adalah bagian dari fungsi rasional pecahan yang penyebutnya merupakan suatu fungsi konstan. Sehingga bisa dituliskan sebagai fungsi rasional pecahan. Tetapi kita tetap menyebutnya sebagai fungsi rasional bulat..

Macam-macam fungsi rasional bulat adalah

-Fungsi konstan dengan bentuk , dengan k adalah suatu konstanta

-Fungsi linear atau fungsi pangkat satu, dengan bentuk dengan a dan b bilangan real dan a tidak sama dengan nol

-Fungsi kuadrat atau fungsi pangkat dua, bentuknya 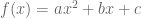 dengan a, b dan c bilangan real dan a tidak sama dengan nol.

-Fungsi pangkat. Bentuknya 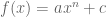. dengan a tidak sama dengan nol. a dan c anggota bilangan real

B. FUNGSI RASIONAL PECAHAN

Fungsi rasional pecahan biasanya disebut sebagai fungsi pecahan adalah fungsi yang peubahnya (biasanya dalam x) terdapat di dalam penyebut suatu pecahan.

dengan  tidak nol dan bukan merupakan fungsi konstan..

beberapa diantaranya adalah

-pembilang dan penyebutnya linear

-pembilang linear, penyebut kuadrat

-pembilang kuadrat, penyebut linear

-pembilang dan penyebut kuadrat

Dan seterusnya...

Contoh fungsi rasional pecahan yang paling dasar adalah 

2. FUNGSI POLINOM

DEFENISI FUNGSI POLINOM : 
Fungsi yang mengandung banyak suku (polinom) dan variabel bebasnya. bentuk umum fungsi polinom : y= a0 + a1x + a2xpangakat 2 + .... + anxpangkat n

contoh polinom adalah : x pangkat 2 - 4x + 7, sedangkan x pangkat 2 - 4/x + 7x3/2 bukan polinom

contoh soal :
 Jika fungsi f(x) = 5x²+4x-8, tentukan nilai fungsi tersebut untuk x = 3

Jawab :

f(3) = 5(3)² + 4(3) – 8

       = 45 + 12 – 8

       = 49

3. FUNGSI LINIER

DEFENISI FUNGSI LINIER : 
Fungsi polinom khusus yang pangkat tertinggi dari variabel bebasnya adalah pangakat 1 (satu). fungsi linier disebut garis lurus yang mempunyai kemiringan.bentuk umum dari fungsi linier y= ao+a1x yang dimana

y = variabel bebas

x = variabel terikat

ao = konstanta

a1 = koefisien

contoh fungsi linear :

Gambarlah grafik y = 2x + 8 !

Selanjutnya, tentukan titik potong dengan sumbu X!

Penyelesaian :

Perhatikan grafik y = 2x + 8 pada gambar di bawah!

Seperti yang terlihat pada grafik, nilai y = 0 saat x = -4.

Dengan demikian, titik potong grafik dengan sumbu X adalah (-4,0). Hal ini dapat diperiksa kebenarannya dengan cara mensubtitusikan y = 0 ke dalam persamaan.

                0 = 2x + 8

                x  = -4

4. FUNGSI KUADRAT

DEFENISI FUNGSI KUADRAT : 

Fungsi polinom yang pangkat tertinggi dari variabelnya adalah pangkat dua juga sering disebut fungsi berdrajat dua.bentuk umumn persamaan kuadrat adalah : ao + a1x + a2 xpangkat2 yang dimana :

ao = konstanta

a1 dan a2 = koefisien

contoh fungsi kuadrat :

Tentukan sumbu simetri fungsi kuadrat y = 5x² - 20x + 1

Pembahasan:

Sumbu simetri suatu fungsi kuadrat dapat dihitung dengan rumus  = -b/2a. dari fungsi kuadrat pada soal diperoleh a=5 dan b=-20

x = -b/2a

x = -(-20) / 2(5)

x= 20/10

x= 2

5. FUNGSI KUBIK

DEFENISI FUNGSI KUBIK : 

Fungsi kubik atau fungsi berderajat tiga ialah fungsi yang pangkat tertinggi dari variabelnya adalah pangkat tiga. Setiap fungsi kubik setidak - tidaknya mempunyai sebuah titik belok (inflextion point), yaitu titik peralihan bentuk kurva dari cekung menjadi cembung atau cembung menjadi cekung. Selain titik belok, sebuah fungsi kubik mungkin pula mempunyai satu titik ekstrim (maksimum atau minimum) atau titik dua ekstrim (maksimum atau minimum). Ada tidaknya titik ekstrim dalam suatu fungsi kubik tergantung pada besarnya nilai-nilai b, c, dan d di dalam persamaannya. Dengan demikian terdapat beberapa kemungkinan mengenai bentuk kurva suatu fungsi kubik. Fungsi-fungsi kubik hanya mempunyai titik belok, tanpa titik ekstrim. 

Bentuk umum = ax3 + bx2 + cx + d = 0  dengan a ≠ 0

Contoh soal =

Tentukan himpunan penyelesaian dari

x3 – 7x2 + 10x  = 0

Jawab =

x3 – 7x2 + 10x  = 0

x(x2 – 7x + 10)  = 0

x(x – 2)(x – 5) = 0

x = 0 atau x = 2 atau x = 5

Jadi himpunan penyelesaiannya adalah {0, 2, 5}

6. FUNGSI BIKUADRAT

DEFENISI FUNGSI BIKUADRAT :

fungsi yang variabel bebasnya merupakan pangkat dari suatu konstanta bukan nol. bentuk umumnya y = n pangkat x  n>0

contoh :

Tentukan himpunan penyelesaian dari : f(x) = 3x³ + 2x² + x - 35

Ditanyakan f(2),dan f(7) !
 

Jawab:

f(x) = 3x³ + 2x² + x - 35

f(2) = 3(2)³ + 2(2)² + 2 - 35
       = 24 + 8 + 2 - 35
       = -1

f(x) = 3x³ + 2x² + x - 35

f(7) = 3(7)³ + 2(7)² + 7 - 35

       = 441 + 98 + 7 - 35

       = 511

7. FUNGSI PANGKAT  

DEFENISI FUNGSI PANGKAT :

fungsi yang variabel bebasnya berpangkat sebuah bilangan nyata bukan nol. bentuk umumnya y = x pangkat n n = bilangan nyata bukan nol.

contoh : 

Nilai pembuat nol fungsi f diperoleh jika f(x) = 0

x^{2 - 4x - 5 = 0}

^{( x - 5 ) ( x + 1 ) = 0}

^{x = 5  v  x = -1}

Jadi pembuat nol fungsi f adalah 5 dan -1 

Untuk x = 0, maka f(0) = -5
x = -2, maka f(-2) = (-2)² - 4(-2) - 5 = 7.

Terima Kasih